參數自適應密化的機器人NURBS曲線運動插補方法與流程
2023-10-18 01:39:14 1
本發明涉及諸如焊接、切割、噴塗、搬運等工業機器人先進位造產業技術領域,特別是涉及一種參數自適應密化的機器人NURBS曲線運動插補方法。
背景技術:
工業機器人控制系統要求能夠在一定的控制策略的作用下,使機器人能夠快速準確地根據預先規劃的軌跡運行,其中,插補算法作為實現工業機器人運動控制的軟體核心,是實現工業機器人複雜軌跡規划算法的基礎,其性能決定著工業機器人運動的實時性和精度的好壞,是工業機器人機器人運動控制特性的重要評價指標之一。
傳統的插補算法主要有直線和圓弧插補等,當需要複雜曲線時,需要通過直線或圓弧的逼近來完成,這種實現方法存在以下問題:①採用直線或圓弧逼近時,會產生大量的端點數據,造成數據量過大;②大量的小線段插補引起進給速度的波動,影響加工效率和精度。
隨著複雜曲線加工需求的增多以及加工精度和效率要求越來越高,曲線插補算法成為研究熱點。其中,NURBS(Non-Uniform Rational B-Spline,非均勻有理B樣條)描述的曲線曲面技術得到重視,並在CNC中得到廣泛研究,也引起了機器人界的關注。NURBS曲線插補算法可以應用於複雜軌跡插補,但計算過程複雜,且機器人關節在加減速過程中存在振動和衝擊。總的來說,上述常用的工業機器人運動軌跡插補方法存在以下問題:1)現有的插補算法應用於複雜曲線插補過程的運動平穩性和運動精度較低,導致目前對於複雜曲線插補問題仍然沒有完善的解決方法;2)現有的NURBS插補算法多採用前瞻方法來確定減速點的位置,只能對減速過程進行規劃,而不能完全保證加速過程的柔順性,無法應用於工業場合;3)現有的插補算法不能解決在曲率變化大的地方,所需減速距離長的情況,導致很難滿足生產過程的安全要求。
技術實現要素:
本發明的目的是為了克服已有的技術缺陷,解決基於三次NURBS曲線的工業機器人運動軌跡插補方法中複雜曲線插補過程的運動平穩性和運動精度較低問題、只能對減速過程進行規劃而不能完全保證加速過程的柔順性問題以及在曲率變化較大的地方所需減速距離較長的問題,本發明提供一種參數自適應密化的機器人NURBS曲線運動插補方法,實現工業機器人高效率、高精度且兼顧柔性的軌跡插補。
本發明採用一種參數自適應密化的機器人NURBS曲線運動插補方法,該方法包括以下步驟:
步驟10)根據輸入的運動參數,獲得NURBS曲線表達式及參數密化過程中採用的導函數表達式;
步驟20)利用改進的Admas微分方程,對步驟10)輸入的運動參數中的節點矢量u進行預估,並根據約束條件,自適應對運動參數中的節點矢量u進行校正;
步驟30)通過分段進行S型曲線位置插補,對自適應過程中的運動參數進行平滑處理;
步驟40)採用球面線性插值slerp方法完成姿態插補,得到的位置插補坐標和姿態插補坐標;
步驟50)對步驟40)得到的位置插補坐標和姿態插補坐標,進行機器人正逆解計算,得到關節角插補序列。
作為優選例:所述的步驟10)具體包括:
步驟101)確定三次NURBS曲線表達式:對於給定的控制頂點{d0,d1,...,dn}及其權值{ω0,ω1,...,ωn}和節點矢量{u0,u1,...,un+k+1},其中,k=3,得到三次NURBS曲線表達式p(u),如式(1)所示:
其中,ωi表示控制頂點di的權值,di表示第i個控制頂點,Ni,3表示3次B樣條基函數,B3、B2、B1和B0分別為分子係數;b3、b2、b1和b0分別為分母係數;
步驟102)求解三次NURBS曲線第i-2段表達式:
令其中3≤j≤n+1,代入式(1),得到式(2):
式中,dj表示第j個控制頂點,ωj表示控制頂點dj的權值,Nj,3表示3次B樣條基函數,di-3表示第i-3個控制頂點,ωi-3表示控制頂點di-3的權值,di-2表示第i-2個控制頂點,ωi-2表示控制頂點di-2的權值,di-1表示第i-1個控制頂點,ωi-1表示控制頂點di-1的權值,di表示第i個控制頂點,ωi表示控制頂點di的權值,上標T表示轉置,
步驟103)求解NUBRS曲線第i-2段表達式的分子係數和分母係數:將Mi代入式(2),得分子係數和分母係數分別為:
步驟104)計算NURBS曲線的導函數表達式:首先在式(2)所示的NURBS曲線表達式上,利用求導公式對節點矢量u求導,獲得NURBS曲線的一階導函數;然後對一階導函數再次利用求導公式對節點矢量u求導,獲得NURBS曲線的二階導函數。
作為優選例:所述的步驟20)具體包括:
步驟201)密化自變量u:
當參數u索引i>2時,根據式(6)預估下一個參數;
當參數u索引1≤i≤2時,採用一階泰勒級數展開,如式(3)所示:
式中,ui+1表示規劃節點矢量,ui表示已知節點矢量,ΔLi表示規劃周期內的步長,T表示規劃周期,表示機器人末端速度,px(u)表示直角坐標系下x軸方向位置插補序列,py(u)表示直角坐標系下y軸方向位置插補序列,pz(u)表示直角坐標系下z軸方向位置插補序列;
根據三步四階Admas微分方程,表示參數密化的遞推公式如式(4)所示:
其中,ui+1表示規劃節點矢量,表示規劃節點矢量的導數,ui表示已知的第i個節點矢量,表示已知的第i個節點矢量的導數,表示已知的第i-1個節點矢量的導數,表示已知的第i-2個節點矢量的導數;
步驟202)用差分代替微分:式(4)中的微分採用式(5)替換為差分,如式(6)所示:
其中,表示預估參數;
步驟203)計算相對誤差:根據預估參數獲得預估點位置坐標並獲得相應的預估步長如式(7)所示:
其中,表示預估步長,表示預估點x軸位置坐標,表示預估點y軸位置坐標,表示預估點z軸位置坐標,xi表示已知點x軸位置坐標,yi表示已知點y軸位置坐標,zi表示已知點z軸位置坐標;
計算預估步長與期望步長ΔLi的相對誤差δi,如式(8)所示:
其中,期望步長ΔLi為自適應步長調節過程中獲得的步長;
步驟204)校正預估參數:如果相對誤差δi超出給定閾值,則採用式(9)對預估參數進行校正:
其中,表示預估的插補點參數;
若預估的插補點數目大於等於1,則對預估的插補點進行位置插補,否則對。
作為優選例:所述的步驟203)中,計算期望步長具體包括:
步驟2031)計算弦高誤差約束:採用式(10)計算弦高誤差:
其中,為預估的插補點參數,ui為已知的插補點參數,pi為ui的插補點坐標,為的插補點坐標,為和ui的中位點坐標,ei為預估點與已知點的距離,為弦高誤差;
設允許的最大弦高誤差為hmax,則最大弦高誤差約束下,允許的最大步長ΔLi1如式(11)所示:
步驟2032)計算最大進給速度約束:在給定最大進給速度vmax約束下,允許的最大步長ΔLi2如式(12)所示:
ΔLi2=vmaxT 式(12)
步驟2033)計算給定最大進給加速度約束:在給定最大進給加速度約束下,允許的步長ΔLi3如式(13)所示,其中,進給加速度不能超過給定最大進給加速度amax;
ΔLi-1-amaxT2≤ΔLi3≤ΔLi-1+amaxT2 式(13)
其中,ΔLi-1表示第i-2插補點和第i-1插補點間的步長;
即步長滿足式(14):
其中,ΔLi表示第i-1插補點和第i插補點間的步長;
如果ΔLi3>ΔLi-1+amaxT2,則令ΔLi3=ΔLi-1+amaxT2;如果ΔLi-1-amaxT2>ΔLi3,則令ΔLi3=ΔLi-1-amaxT2;
步驟2034)計算給定最大法向加速度約束:
首先根據NURBS插補過程中進給速度vi與法向加速度ani的關係,採用式(15)計算法向加速度ani:
式中,ρi表示ΔLi的曲率半徑;
設允許的最大法向加速度為anmax,採用式(16)獲得最大法向加速度約束下允許的最大步長ΔLi4:
根據式(15)和式(16),得出即最大法向加速度約束下允許的最大步長為ΔLi4,如式(17)所示:
步驟2035)步長自適應優化調節:在自適應步長規划過程中,當前段的期望步長ΔLi滿足式(18):
通過上述自適應步長調節獲得一系列期望步長序列,然後選取步長序列中的極小值點作為曲率最大的點,即拐點,最後根據獲得的拐點將期望步長序列分成若干段,並記錄每段的總長度,以及拐點處的期望步長。
作為優選例:所述的步驟30)具體包括:首先根據拐點步長和各段的長度,對每段採用七段式S曲線速度規劃,獲得速度序列,從而得到各個周期的進給步長;然後再次通過參數密化過程獲得參數u序列;最後每隔插補周期T'取參數u,獲得在直角坐標系下的位置插補序列p(u)。
作為優選例:所述的步驟40)具體包括:
步驟401)採用四元數表示姿態:將起點、終點姿態以及中間插補姿態採用四元數的表示形式,記法如下:
[r,q]=[r,(R,P,Y)]
其中,r為姿態插補係數,取值範圍為[0,1];q為姿態向量;R為插補點的α旋轉軸的姿態值,P為插補點的β旋轉軸的姿態值,Y為插補點的γ旋轉軸的姿態值;
步驟402)選定姿態插補係數r:將已完成位置插補的總步長之和與NURBS曲線的總長作為姿態插補係數r;
步驟403)採用slerp插補方法完成姿態插補,如式(19)所示:
qr=k0qbeg+k1qend 式(19)
其中,qr表示係數r的姿態向量,qbeg表示起始姿態向量,qend表示終止姿態向量,k0表示起始點係數,k1表示終止點係數;
ω表示qbeg到qend弧所截的角;
採用式(20)所示slerp插補方法完成姿態插補:
作為優選例:所述步驟50)具體為:首先根據位置插補坐標和姿態插補坐標,經機器人正逆解計算得到對應的關節角插補序列,然後將該序列發送給伺服控制器,以控制機器人完成相應的運動操作。
有益結果:本發明採用參數自適應密化的方法有效地解決了NURBS曲線插補加減速過程的柔順性問題以及曲率變化較大的地方所需減速距離較長的問題,通過改進的Adams微分方程方法及自適應步長調節對參數進行預估-校正,從弦高誤差、給定最大進給速度、給定最大進給加速度和給定最大法向加速度四個約束條件下獲得步長序列,提高了預估參數的精度,通過規劃周期T與插補周期T'不同的方式,對自適應參數密化過程進行進一步密化,降低規劃誤差。結合S型曲線速度規劃方法對運動參數進行分段平滑處理,極大的降低了計算量的同時保證了計算精度,實現了柔性加減速。此方法簡單高效,能夠滿足工業機器人在複雜曲線插補過程中的的運動平穩性和運動精度的需求,提高機器人的工作效率和柔性加工能力,具有廣闊的應用前景和良好的經濟效益。
附圖說明
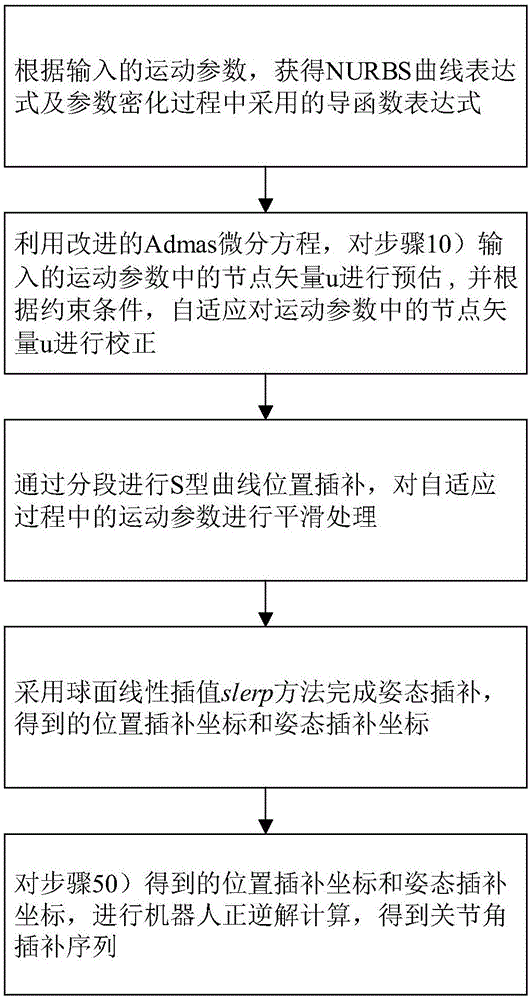
圖1為本發明實施例的流程圖;
圖2為本發明實施例中步驟10)的流程圖;
圖3為本發明實施例中步驟20)和步驟30)的流程圖;
圖4為本發明實施例中步驟20)參數密化校正過程示意圖;
圖5為本發明實施例中步驟203)的流程圖;
圖6為本發明實施例中步驟2031)中弦高誤差示意圖;
圖7為本發明實施例中步驟2031)中弦高誤差計算方法對比示意圖;
圖8為本發明實施例中步驟40)的流程圖。
具體實施方式
下面結合附圖和具體實施方式對本發明做進一步說明。
如圖1所示,本發明的一種參數自適應密化的機器人NURBS曲線運動插補方法,包括以下步驟:
步驟10)根據輸入的運動參數,獲得NURBS曲線表達式及參數密化過程中採用的導函數表達式。
步驟10)首先根據給定的NURBS控制頂點及其權值、節點矢量等參數確定三次NURBS曲線的表達式形式;其次選擇合理的時間間隔,確定每段NURBS曲線的表達式;然後求解每段NURBS曲線的分子分母係數;最後在NURBS曲線表達式的基礎上,獲得NURBS曲線的一階和二階導函數表達式。步驟10)可以以降低插補階段任務計算量。如圖2所示,所述的步驟10)具體包括步驟101)至步驟104):
步驟101)確定三次NURBS曲線表達式:對於給定的控制頂點{d0,d1,...,dn}及其權值{ω0,ω1,...,ωn}和節點矢量{u0,u1,...,un+k+1},其中,k=3,得到三次NURBS曲線表達式p(u),如式(1)所示:
其中,ωi表示控制頂點di的權值,di表示第i個控制頂點,Ni,3表示3次B樣條基函數,B3、B2、B1和B0分別為分子係數;b3、b2、b1和b0分別為分母係數;
步驟102)求解三次NURBS曲線第i-2段表達式:
令其中3≤j≤n+1,代入式(1),得到式(2):
式中,dj表示第j個控制頂點,ωj表示控制頂點dj的權值,Nj,3表示3次B樣條基函數,di-3表示第i-3個控制頂點,ωi-3表示控制頂點di-3的權值,di-2表示第i-2個控制頂點,ωi-2表示控制頂點di-2的權值,di-1表示第i-1個控制頂點,ωi-1表示控制頂點di-1的權值,di表示第i個控制頂點,ωi表示控制頂點di的權值,上標T表示轉置,
步驟103)求解NUBRS曲線第i-2段表達式的分子係數和分母係數:將Mi代入式(2),得分子係數和分母係數分別為:
步驟104)計算NURBS曲線的導函數表達式:首先在式(2)所示的NURBS曲線表達式上,利用求導公式對節點矢量u求導,獲得NURBS曲線的一階導函數;然後對一階導函數再次利用求導公式對節點矢量u求導,獲得NURBS曲線的二階導函數。
步驟20)利用改進的Admas微分方程,對步驟10)輸入的運動參數中的節點矢量u進行預估,並根據約束條件,自適應對運動參數中的節點矢量u進行校正。
步驟20)首先對NURBS曲線表達式的自變量u採用Admas微分方程法進行密化;然後採用差分代替微分法以降低計算量;最後根據預估步長與期望步長的相對誤差對預估參數進行校正以保證計算精度。如圖3所示,所述的步驟20)具體包括:
步驟201)密化自變量u:
當參數u索引i>2時,根據式(6)預估下一個參數;
當參數u索引1≤i≤2時,採用一階泰勒級數展開,如式(3)所示:
式中,ui+1表示規劃節點矢量,ui表示已知節點矢量,ΔLi表示規劃周期內的步長,T表示規劃周期,表示機器人末端速度,px(u)表示直角坐標系下x軸方向位置插補序列,py(u)表示直角坐標系下x軸方向位置插補序列,pz(u)表示直角坐標系下x軸方向位置插補序列;
當精度要求高時,泰勒級數展開需要高階求導,計算複雜,因此根據三步四階Admas微分方程,表示參數密化的遞推公式如式(4)所示:
其中,ui+1表示規劃節點矢量,表示規劃節點矢量的導數,ui表示已知的第i個節點矢量,表示已知的第i個節點矢量的導數,表示已知的第i-1個節點矢量的導數,表示已知的第i-2個節點矢量的導數;
步驟202)用差分代替微分:式(4)中的微分採用式(5)替換為差分,如式(6)所示:
其中,表示預估參數;
步驟203)計算相對誤差:根據預估參數獲得預估點位置坐標並獲得相應的預估步長如式(7)所示:
其中,表示預估步長,表示預估點x軸位置坐標,表示預估點y軸位置坐標,表示預估點z軸位置坐標,xi表示已知點x軸位置坐標,yi表示已知點y軸位置坐標,zi表示已知點z軸位置坐標;
計算預估步長與期望步長ΔLi的相對誤差δi,如式(8)所示:
其中,期望步長ΔLi為自適應步長調節過程中獲得的步長;
步驟204)校正預估參數:如圖4所示,如果相對誤差δi超出給定閾值,則採用式(9)對預估參數進行校正:
其中,表示預估的插補點參數;
若預估的插補點數目大於等於1,則對預估的插補點進行位置插補。
在步驟203)中,根據約束條件,自適應對運動參數中的節點矢量u進行校正。
步驟203)首先採用自適應步長調節的方法,根據弦高誤差、給定最大進給速度、給定最大進給加速度和給定最大法向加速度等四個約束條件,對步長進行自適應優化調節;然後通過選取拐點將步長序列分為若干段。如圖5所示,所述的步驟203)具體包括步驟2031)至步驟2035):
步驟2031)計算弦高誤差約束:弦高誤差是指以直線代替曲線的所產生的誤差,如圖6所示。本發明採用式(10)所示的近似方法計算弦高誤差,即近似等於如圖7中所示的弧長ε。
其中,為預估的插補點參數,ui為已知的插補點參數,pi為ui的插補點坐標,為的插補點坐標,為和ui的中位點坐標,εi為預估點與已知點的距離,為弦高誤差;
設允許的最大弦高誤差為hmax,則最大弦高誤差約束下,允許的最大步長ΔLi1如式(11)所示:
步驟2032)計算最大進給速度約束:在給定最大進給速度vmax約束下,允許的最大步長ΔLi2如式(12)所示:
ΔLi2=vmaxT 式(12)
步驟2033)計算給定最大進給加速度約束:在給定最大進給加速度約束下,允許的步長ΔLi3如式(13)所示,其中,進給加速度不能超過給定最大進給加速度amax;
ΔLi-1-amaxT2≤ΔLi3≤ΔLi-1+amaxT2 式(13)
其中,ΔLi-1表示第i-2插補點和第i-1插補點間的步長;
即步長滿足式(14):
其中,ΔLi表示第i-1插補點和第i插補點間的步長;
如果ΔLi3>ΔLi-1+amaxT2,則令ΔLi3=ΔLi-1+amaxT2;如果ΔLi-1-amaxT2>ΔLi3,則令ΔLi3=ΔLi-1-amaxT2;
步驟2034)計算給定最大法向加速度約束:
首先根據NURBS插補過程中進給速度vi與法向加速度ani的關係,採用式(15)計算法向加速度ani:
式中,ρi表示ΔLi的曲率半徑;
設允許的最大法向加速度為anmax,採用式(16)獲得最大法向加速度約束下允許的最大步長ΔLi4:
根據式(15)和式(16),得出即最大法向加速度約束下允許的最大步長為ΔLi4,如式(17)所示:
步驟2035)步長自適應優化調節:在自適應步長規划過程中,當前段的期望步長ΔLi滿足式(18):
通過上述自適應步長調節獲得一系列期望步長序列,然後選取步長序列中的極小值點作為曲率最大的點,即拐點,最後根據獲得的拐點將期望步長序列分成若干段,並記錄每段的總長度,以及拐點處的期望步長。
步驟30)通過分段進行S型曲線位置插補,對自適應過程中的運動參數進行平滑處理。
步驟30)可以實現柔性加減速。步驟30)具體包括:首先根據拐點步長和各段的長度,對每段採用七段式S曲線速度規劃,獲得速度序列,從而得到各個周期的進給步長;然後再次通過參數密化過程獲得參數u序列;最後每隔插補周期T'取參數u,獲得在直角坐標系下的位置插補序列p(u)。
步驟40)採用球面線性插值slerp方法完成姿態插補,得到的位置插補坐標和姿態插補坐標。
步驟40)採用球面線性插值slerp(Spherical Linear Interpolation)完成姿態插補,首先將起點、終點姿態以及中間插補姿態採用四元數的表示形式;然後將已完成位置插補的總步長之和與NURBS曲線的總長作為姿態插補參數r;最後根據起點和終點的姿態採用slerp插補方法完成NURBS姿態插補。如圖8所述,所述的步驟40)具體包括步驟401)至步驟403):
步驟401)採用四元數表示姿態:將起點、終點姿態以及中間插補姿態採用四元數的表示形式,記法如下:
[r,q]=[r,(R,P,Y)]
其中,r為姿態插補係數,取值範圍為[0,1];q為姿態向量;R為插補點的a旋轉軸的姿態值,P為插補點的β旋轉軸的姿態值,Y為插補點的γ旋轉軸的姿態值;
步驟402)選定姿態插補係數r:將已完成位置插補的總步長之和與NURBS曲線的總長作為姿態插補係數r;
步驟403)採用slerp插補方法完成姿態插補,如式(19)所示:
qr=k0qbeg+k1qend 式(19)
其中,qr表示係數r的姿態向量,qbeg表示起始姿態向量,qend表示終止姿態向量,k0表示起始點係數,k1表示終止點係數;
ω表示qbeg到qend弧所截的角;
採用式(20)所示slerp插補方法完成姿態插補:
步驟50)對步驟40)得到的位置插補坐標和姿態插補坐標,進行機器人正逆解計算,得到關節角插補序列。
所述步驟50)具體為:首先根據位置插補坐標和姿態插補坐標,經機器人正逆解計算得到對應的關節角插補序列,然後將該序列發送給伺服控制器,以控制機器人完成相應的運動操作。
應當指出,對於本技術領域的普通技術人員來說,在不脫離本發明原理的前提下,還可以做出若干改進和潤飾,這些改進和潤飾也應視為本發明的保護範圍。本實施例中未明確的各組成部分均可用現有技術加以實現。
