水文序列均值跳躍變異的識別與分級方法與流程
2023-12-07 02:36:16 3
本發明涉及一種基於相關係數的水文序列均值跳躍變異的識別與分級方法。
技術背景
近年來,氣候變化與人類活動對流域下墊麵條件的影響所引起的水文效應,逐漸成為全球水循環變化研究的焦點問題。在此變化環境下,水文序列將不再認為來自同一總體,失去了原有的一致性。因此,水資源評價、規劃、管理等應基於對變化環境下水文序列的非一致性成分分析之上。
對於存在跳躍變異的水文序列而言,目前關於時間序列跳躍變異的研究主要側重於跳躍點的識別。然而,在非一致性的工程水文計算中,不僅需要對序列發生跳躍變異的時間、次數等進行識別與檢驗,還需要對其變異程度進行描述與分級量化,從而更全面地為開展流域環境變化及其影響評價提供依據。然而,目前針對水文序列跳躍變異分級的研究尚少,尚未提出一種有效的方法,既可識別跳躍點又可對跳躍變異程度進行分級描述,遠無法滿足實際需求。
為此,從序列產生跳躍變異的實質出發,取跳躍性成分與原始序列的相關係數作為跳躍變異的識別與分級指標,提出一種既可對水文序列變異點進行高效率的識別與檢驗,又可對變異程度進行定量描述與分級的方法,從而為水資源評價與規劃提供更全面更可靠的依據。
技術實現要素:
本發明是為了解決上述問題而進行的,目的在於提供一種基於相關係數的水文序列均值跳躍變異的識別與分級方法。
本發明為了實現上述目的,採用了以下方案:
本發明提供一種水文序列均值跳躍變異的識別與分級方法,其特徵在於,包括以下步驟:步驟1.水文序列均值變異點識別與檢驗:對水文序列x從起點至終點範圍內進行滑動識別,並且假設滑動起點為變異點,逐點滑動,依次求取各假設變異點對應的跳躍成分序列y與原始序列x的相關係數r,取所有結果中絕對值最大的相關係數|rmax|,對其進行假設檢驗,若通過,則認為|rmax|所對應的假設變異點為水文序列變異點;步驟2.水文序列跳躍變異分級:考慮相關係數假設檢驗的顯著性水平、水文序列對長度的要求、相關分析對相關性大小的要求等,確定相關係數閾值,將跳躍變異程度劃分為5級:0≤|r|<rα,級別為無變異;rα≤|r|<rβ,級別為弱變異;rβ≤|r|<0.6,級別為中變異;0.6≤|r|<0.8,級別為強變異;0.8≤|r|≤1.0,級別為巨變異。
本發明提供的水文序列均值跳躍變異的識別與分級方法,還可以具有以下特徵:
步驟1包括以下子步驟:
子步驟1-1.求取相關係數絕對值|r|:
對於長度為n的序列x={xi},通過跳躍變異診斷得到其變異點位置後,將整個序列分割成長度分別為n1和n2的兩段子序列,求得序列均值為前後兩個子序列均值分別為和
構造一個跳躍成分組成的序列y={yi},(i=1,2,...,n1);(j=n1+1,n1+2,...,n),則跳躍成分序列的均值可表示為:
原始序列x與跳躍成分y具有一定的相關關係,其相關係數r為:
簡化後可得:
在上式中,
子步驟1-2.假設檢驗:
從水文序列x中各個各假設變異點所對應的相關係數中選取絕對值最大的相關係數|rmax|,對其進行假設檢驗,從常用的顯著水平0.01,0.02,0.05和0.1中取α,若|rmax|<rα,說明未通過假設檢驗,則該序列無跳躍變異點;若|rmax|>rα,說明通過假設檢驗,則認為|rmax|所對應的假設變異點為該水文序列的變異點。
本發明提供的水文序列均值跳躍變異的識別與分級方法,還可以具有以下特徵:步驟2包括以下內容:對相關係數進行假設檢驗,從常用的顯著水平0.01、0.02、0.05、0.1中取α與β(α>β)分別進行檢驗;若r未通過顯著水平為α的檢驗,則說明此顯著水平下變異不顯著,將其劃分為無變異級別;若通過了顯著水平為α的檢驗但未通過顯著水平為β的檢驗,則劃分為弱變異級別;若通過顯著水平為β的檢驗,則說明變異較為顯著,可再細化分級;當資料長度取水文計算要求的最短值20時,常用顯著水平下的最大閾值均小於0.6,則對於rβ≤|r|<0.6,將其變異程度劃分為中變異級別;相關係數|r|≥0.8,則劃分為巨變異級別;而0.6≤|r|<0.8時,則劃分為強變異級別。
發明的作用與效果
本發明從序列產生跳躍變異的實質出發,取跳躍性成分與原始序列的相關係數作為跳躍變異的識別與分級指標,提出一種既可對水文序列變異點進行高效率的識別與檢驗,又可對變異程度進行定量描述與分級的方法,從而為水資源評價與規劃提供更全面更可靠的依據。
附圖說明
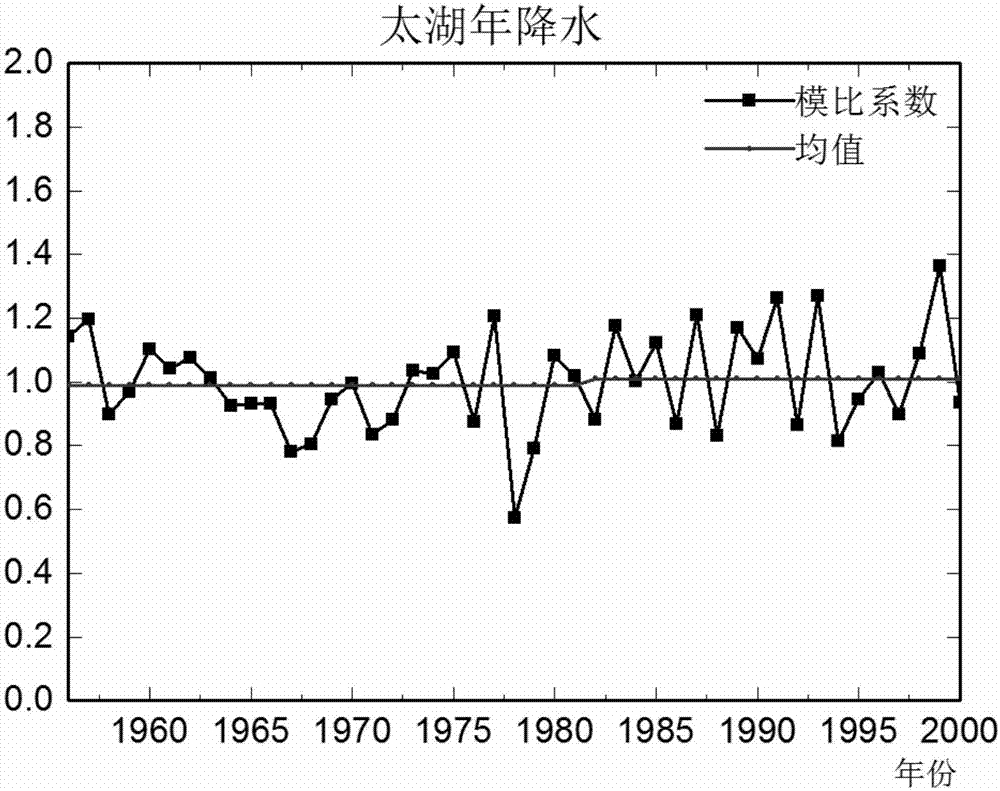
圖1為本發明實施例所涉及的實測太湖年降水序列跳躍變異情況示意圖;
圖2為本發明實施例所涉及的實測太湖年徑流序列跳躍變異情況示意圖;
圖3為本發明實施例所涉及的實測沱江年降水序列跳躍變異情況示意圖;
圖4為本發明實施例所涉及的實測開孔河年降水序列跳躍變異情況示意圖;以及
圖5為本發明實施例所涉及的實測博羅站年水位序列跳躍變異情況示意圖。
具體實施方式
以下結合附圖對本發明涉及的水文序列均值跳躍變異的識別與分級方法的具體實施方案進行詳細地說明。
如圖1所示,本實施例所提供的水文序列均值跳躍變異的識別與分級方法包括以下步驟:
步驟1.水文序列均值變異點識別與檢驗:
對水文序列x從起點至終點範圍內進行滑動識別,並且假設滑動起點為變異點,逐點滑動,依次求取各假設變異點對應的跳躍成分序列y與原始序列x的相關係數r,取所有結果中絕對值最大的相關係數|rmax|,對其進行假設檢驗,若通過,則認為|rmax|所對應的假設變異點為水文序列變異點;具體包括以下子步驟:
子步驟1-1.求取相關係數絕對值|r|:
對於長度為n的序列x={xi},通過跳躍變異診斷得到其變異點位置後,將整個序列分割成長度分別為n1和n2的兩段子序列,求得序列均值為前後兩個子序列均值分別為和
構造一個跳躍成分組成的序列y={yi},(i=1,2,...,n1);(j=n1+1,n1+2,...,n),則跳躍成分序列的均值可表示為:
原始序列x與跳躍成分y具有一定的相關關係,其相關係數r為:
無論該序列的跳躍變異程度如何,均可求得此相關係數r,且取值範圍為±1,表明r具有易求解和便於比較的屬性;
由相關係數定義式可知,公式(5)中r主要是反映了原始序列與跳躍成分的相關程度,為更加明確地闡明其具有表徵跳躍變異程度的能力,對與r的關係進行推導。
將式(5)中分子分母各項用表示如下:
式中:
將式(6)-(9)代入式(5)並簡化可得:
子步驟1-2.假設檢驗:
對於存在均值跳躍變異的序列而言,在一定離散程度下,所識別出的變異點應使得變異點前後子序列均值之差儘可能大。由式(11)可知,相關係數的絕對值可以反映上述變異點識別的基本條件。由此提出利用水文序列的相關係數進行滑動檢驗的設想:對於變異點未知的序列,假設滑動起點為變異點,逐點滑動,依次求取各假設變異點對應的跳躍成分序列y與原始序列x的相關係數。
取水文序列x中各假設變異點所對應的相關係數中絕對值最大的相關係數|rmax|,對其進行假設檢驗。從常用的顯著水平0.01,0.02,0.05和0.1中取α,若|rmax|<rα,說明未通過假設檢驗,則該序列無跳躍變異點;若|rmax|>rα,說明通過假設檢驗,則認為|rmax|所對應的假設變異點為該水文序列的變異點。此外,考慮到假設變異點的位置若過於靠近首端或尾端會使得子序列樣本容量太小,導致抽樣誤差太大,結果不可靠,因此滑動檢測通常不從序列起點開始。
步驟2.水文序列跳躍變異分級
對相關係數進行假設檢驗,從常用的顯著水平0.01、0.02、0.05、0.1中取α與β(α>β)分別進行檢驗;若r未通過顯著水平為α的檢驗,則說明此顯著水平下變異不顯著,將其劃分為無變異級別;若通過了顯著水平為α的檢驗但未通過顯著水平為β的檢驗,則劃分為弱變異級別;若通過顯著水平為β的檢驗,則說明變異較為顯著,可再細化分級;
另外,當資料長度取水文計算要求的最短值20時,常用顯著水平下的最大閾值均小於0.6,則對於rβ≤|r|<0.6,將其變異程度劃分為中變異級別;在對水文序列進行相關分析時,通常要求相關係數|r|≥0.8,因為此時相關係數可以通過常用顯著水平的顯著性檢驗,說明兩變量之間線性關係顯著,從變異的角度來看,原序列與跳躍成分序列相關顯著,則說明序列跳躍變異非常顯著,因此可將其變異程度劃分為巨變異級別;而0.6≤|r|<0.8時,則劃分為強變異級別。
本實施例中,採用上述水文序列均值跳躍變異識別與分級方法,在顯著水平α=0.05,β=0.01的條件下,首先對瀾滄江下遊允景洪水文站多時間尺度徑流序列進行變異點識別。同時採用pettitt檢驗法與brown-forsythe檢驗法作為對比,可知本方法在實際水文序列的變異點識別檢驗中有較為理想的效果。變異點識別結果及識別效率如下表1所示:
表1.允景洪站多時間尺度徑流序列變異點識別檢驗結果表
註:「↑」「↓」表示跳躍變異方向;「-」表示無顯著變異點。
此外,對多個中國水資源二級區、三級區的降雨徑流序列及東江下遊博羅站年水位序列進行變異分級。利用上述分級方法,求得各序列的相關係數值。在顯著性水平α=0.05、β=0.01條件下,得到跳躍變異分級對應的上下限,其中rα=0.294,rβ=0.380。對各實測序列跳躍變異程度進行分級,結果如下表2所示:
表2.多站實測水文序列均值跳躍變異分級結果
註:+表示變異點顯著性較強,﹣表示較弱。
檢測出的太湖年降水序列跳躍變異點的顯著性較弱,其相關係數僅為0.274,小於rα(0.294),因此認為該序列未發生跳躍變異。但太湖年徑流序列的相關係數為0.360,滿足rα≤|r|<rβ,表明該序列發生微弱向上的跳躍變異。沱江年降水序列的相關係數為-0.516,負值表明跳躍變異方向向下,其絕對值滿足rβ≤|r|<0.6,也表明該序列的跳躍變異程度較明顯。開孔河年降水序列的相關係數為0.659,絕對值落在區間[0.600,0.800),對應強烈的向上跳躍變異。博羅站水位序列的相關係數為-0.919,其絕對值遠大於0.800,表明跳躍變異已達到巨變異程度,且方向向下。各序列跳躍變異分級如圖1至5所示。
綜上,水文序列均值跳躍變異識別與分級方法是從序列產生跳躍變異的實質出發,在原理上體現出水文序列變異點前後均值跳躍變異幅度、離散程度等性質,是一種既可對水文序列變異點進行高效率的識別與檢驗,又可對變異程度進行定量描述與分級的方法,計算簡便,結果可靠,可操作性強,具有很大的實際應用價值。
以上實施例僅僅是對本發明技術方案所做的舉例說明。本發明所涉及的水文序列均值跳躍變異的識別與分級方法並不僅僅限定於在以上實施例中所描述的內容,而是以權利要求所限定的範圍為準。本發明所屬領域技術人員在該實施例的基礎上所做的任何修改或補充或等效替換,都在本發明的權利要求所要求保護的範圍內。
