123澳門正版資料1877（123澳門正版免費資料大全）

2024-07-11 18:24:48

123澳門正版資料1877是一份查詢澳門各種數學公式的資料，數學公式是人們在研究自然界物體和物體之間的關係時，發現的某種通過特定方式表達出來的聯繫，也對自然界中不同事物之間的數量進行了比較清晰地表徵，這些公式能幫助學習數學的人，更好地認識自然界中存在的規律，理解事物的本質與內涵。

學會辨別公式是否正確
公式能幫助人們更好地認識自然規律，加深對客觀事物的了解，需要學會辨別正確的和錯誤的公式，常見的錯誤公式通常存在以下幾個特徵：
1.自稱是科學的公式，但是描述難以做到準確具體，甚至沒有明確的度量衡。
2.沒有明確的操作定義，就是描述的對象並不具體，難以做到客觀，外人沒有檢驗的依據或者途徑。
3.透露出來的數學原理比較囉嗦，不是最簡潔的數學道理，出現眾多變量的情況下，不能通過最簡單的方式得出問題的答案。
4.描述方式比較曖昧，為了增強公式的可信度，使用大量的專業術語製造閱讀壁壘。
5.沒有邊界條件，一種嚴謹的科學公式表達方式應該闡明在某些具體的情況下這條原理適用，還有在哪些範圍之外原理並不適用。
基本常識公式
小學階段很多人都是從公式開始接觸數學，最早開始認識物體就是從這個物體的周長和面積等數據入手，常見的周長公式有
長方形的周長 = （長+寬）×2 = 2（a+b） = （a+b）×2
正方形的周長 = 邊長×4 = 4a
圓的周長 = 圓周率×直徑 = π d = 圓周率×半徑×2 = 2 π r

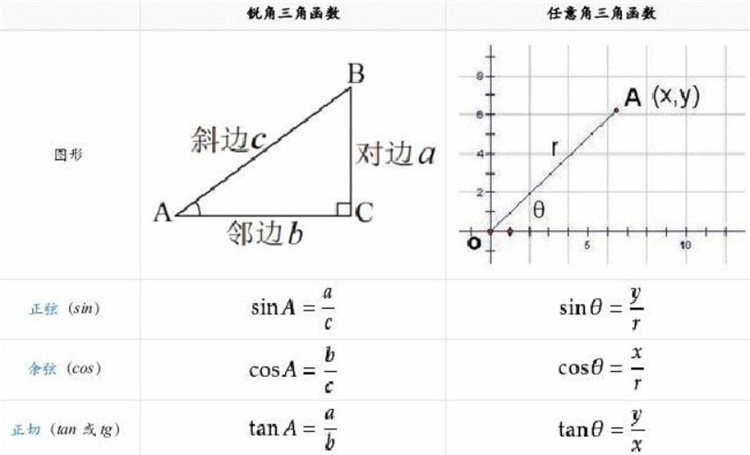
這些公式在學生小學階段就已經初步掌握並且進行相應的練習，還會對長方形、正方形和圓形的面積進行了解，隨著學習程度的深入，學生還會掌握一些常見幾何體的體積計算方式，這些數學公式為人們認識物體、計算物體的具體數據提供了詳細的參考資料，加深了人類對事物的了解。
三角公式
弧度制下的角的表示：
sin（2kπ+α）=sinα （k∈Z）
cos（2kπ+α）=cosα （k∈Z）
tan（2kπ+α）=tanα （k∈Z）
cot（2kπ+α）=cotα （k∈Z）
sec（2kπ+α）=secα （k∈Z）
csc（2kπ+α）=cscα （k∈Z）
角度制下的角的表示：
sin (α+k·360°)=sinα（k∈Z）
cos(α+k·360°)=cosα（k∈Z）
tan (α+k·360°)=tanα（k∈Z）
cot（α+k·360°）=cotα （k∈Z）
sec（α+k·360°）=secα （k∈Z）
csc（α+k·360°）=cscα （k∈Z）
弧度制下的角的表示：
sin（π+α）=－sinα （k∈Z）
cos（π+α）=－cosα（k∈Z）
tan（π+α）=tanα（k∈Z）
cot（π+α）=cotα（k∈Z）
sec（π+α）=－secα（k∈Z）
csc（π+α）=－cscα（k∈Z）

三角公式主要是對組成三角形的三個角總結歸納出的一系列公式，由於內角和為180度，再加上有比較明顯的對邊和鄰邊關係，就有人總結出這種具有明顯規律性的公式，不管是對於三個角度大小的推導還是對三條邊長度關係的解析，都能通過這些三角公式計算出來，正餘弦定理和秦九韶公式對於計算三角形的邊長與面積具有很重要的作用，這些公式是都是在三角形的基礎之上推導出來的，換到其他的圖形裡面就不再適用。
解析公式
在解析幾何當中，圓、橢圓和拋物線、反比例函數等等都在坐標系裡面被賦予了更多樣的數學應用場景，圓和拋物線都有對應的解析幾何表達式，還有標準方程方便數學學習者更方便地觀察出表達式的特徵，在平面直角坐標系裡面，拋物線的基本公式是y=ax²+bx+c，其中a大於零時拋物線的開口向上，小於零時開口向下，c的取值也會影響拋物線和y軸交點正負方向的關係，數學有很多值得研究的有趣規律，解析公式更是需要花費很多工夫才能深入了解。
概率邏輯歸納
概率學分析中對於概率的計算有明確的公式，p（A）=m/n，其中p是事件發生的概率，A是需要計算的事件，n是所有可能發生的事件數量，m是事件A的數量個數，另外還有一種條件概率，適用在某種條件達成的情況下計算對應的事件概率，根據具體的計算方式分為古典概型和幾何概型，數學是人類認知自然規律的一種重要方式，如今也正在有很多最新的數學公式在被創造出來，探索未知的腳步從未停止。