指數對數的判斷方法（關於指數和對數的證明問題）

2023-09-16 20:31:27 1

指數對數的判斷方法?1.已知a^x•b^y•c^z=a^y•b^z•c^x=，下面我們就來聊聊關於指數對數的判斷方法?接下來我們就一起去了解一下吧!

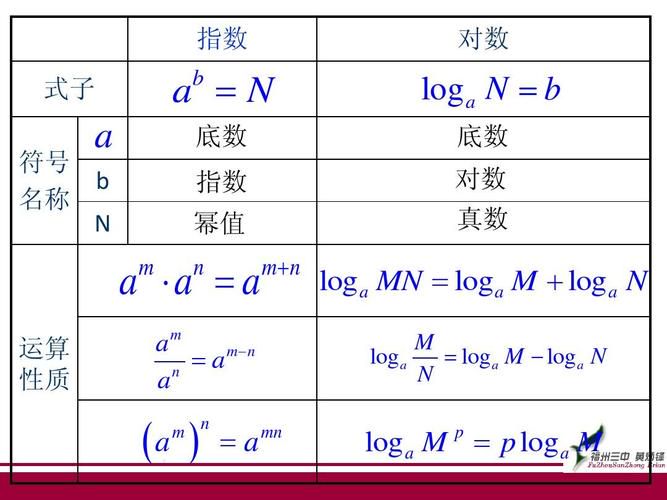
指數對數的判斷方法

1.已知a^x•b^y•c^z=a^y•b^z•c^x=

a^z•b^x•c^y=1(a,b,c>1),求證：

x y z=0

證明：根據指數與對數的計算特點，先對已知的式子兩邊同時取對數，使指數上不含有字母。記

lga=A,lgb=B,lgc=C.又因為a,b,c>1,所以

A,B,C>0.由題意設有：

lg(a^x•b^y•c^z)=lg(a^y•b^z•c^x)

=lg(a^z•b^x•c^y)=0,

即 Ax By Cz=0,

Bx Cy Az=0,

Cx Ay Bz=0.

將上面的三個式子相加，可得：

（A B C)(x y z)=0

因為A B C>0,所以x y z=0.

2.對於正整數a,b,c(a<=b<=c)和實數x,y,z,w,若a^x=b^y=c^z=70^w,

1/x 1/y 1/z=1/w.

求證：a b=c.

證明：由a^x=b^y=c^z=70^w,可得：

a^(1/w)=70^(1/x), b^(1/w)=70^(1/y),

c^(1/w)=70^(1/z).

所以，(abc)^(1/w)=70^(1/x 1/y 1/z),

abc=70.

因為x,y,z,w均不等於0,可從a^x=b^y=c^z

=70^w不等於1知道a,b,c均不為1，又因70=2×5×7，而2，5，7為質數，所以70=

2×5×7是分解因數的唯一方法。由於abc

=70,a<=b<=c,所以：a=2,b=5,c=7,

故此a b=c.

3.已知A=6lgp lgq,其中p,q為質數，且滿足q-p=29,求證：3<A<4.

證明：從p,q為質數且滿足q-p=29,可得知：p與q必是為一奇一偶，不可能是兩個都是奇數，而既是偶數又是質數的數只有2，故此p=2,那麼q=31.

A=6lgp lgq=6lg2 lg31=lg(2^6×31)

=lg1984.

因為1000<1984<10000,所以

lg1000<lg1984<lg10000,

即3<A<4.

4.證明：[(✓65)-8]^100的小數表示式中第一個有效數字前至少有121個零(lg2=0.3010).

證明：因為0<(✓65)-8=1/(✓65)-8<1/(8 8)=1/16,

所以：0<[(✓65)-8]^100<16^(-100).

lg[(✓65)-8]^100<lg16^(-100)=-100×

4lg2.

=-400×0.3010=-120.4

因此，[(✓65)-8]^100的小數表示式中第一個有效數字前面至少有121個零。