傅立葉變換最通俗的理解秒懂（有人能講明白傅立葉變換了）

2023-09-18 00:50:33 5

傅立葉變換，一度被推上了玄學的位置。

這位說，了解了它，能改變你，認識世界的方式。那個說，我喜歡信號系統，但是看了2周的傅立葉變換，放棄了。

也有很多人，寫了科普教程，有零基礎教程、保證看懂教程、掐死教程。但是，當他們亮出數學公式的那一刻，很多人陷入沉思：我……是從哪裡開始，就已經看不懂了……

這些現象，激發了我強烈的表演欲望，我要登上舞臺，為大家表演。我的表演，如果你看不懂，請掐死我。

我正寫博客，此時正是深夜，我屋內的電腦，發出「嗡嗡」的散熱聲。同時，窗外的馬路，飛馳而過一輛渣土車，發出「嘀~」一聲刺耳的鳴笛。

我，是如何，聽到，聲音的。

物體振動發出的聲音，在空氣中傳播，進入我的耳朵，推動我的耳膜，聲音大就推得強，聲音小就推的弱，經過一系列處理，我就聽到了電腦和汽車。

仔細想一下，有點奇怪，我居然根據耳膜被推動的情況，分析出了聲音裡，包含電腦散熱風扇和汽車喇叭兩種物體。其實除此之外，我還聽到了樓上放電視、窗外的蟲子叫、電動車報警器響了……

這個聲音發出和接收的場景，就如同你用手指在桌子上有規律、有輕重地敲擊。我相信，你能聽出這番敲擊是打快板，那番敲擊是非洲鼓。但是，你很難通過敲桌子的節奏，聽出來：你的同事在敲鍵盤，同時路上響起了救護車的聲音。

先給你3分鐘的時間思考一下，我去上個廁所先。

人類幾萬年的歷史，不知道是否有人想過這個問題，拿根棍子捅你的耳膜，你就能分辨出十幾樣不同的發聲物體，這到底該怎麼來解釋呢？

其實，這——就是傅立葉變換（我能讓你猜著，這突然地轉場？）。

如下圖所示：推動你耳膜的力度就是左側的波形，你的大腦經過傅立葉變換，分析出了十幾種不同的發聲物體。

好了，現在拿出傅立葉變換的定義：

傅立葉變換，表示能將滿足一定條件的某個函數表示成三角函數（正弦和/或餘弦函數）或者它們的積分的線性組合。

定義看不懂沒關係，只要能看懂前面說的，分辨聲音的那個例就行。

關於什麼是傅立葉，此處打個標記叫[A]。如果你看不懂，就說從[A]開始就糊塗了，來掐我時，好讓我死得明白。

但是，有一點談資我們要知道，這個理論是法國人傅立葉在1807年提出來的。那時，嘉慶皇帝剛抄了和珅的家沒過幾年。

三、描述一個波：都有獨特的氣質

你糊弄我？你拿人這種有靈性的生物，來舉數學的例子，數學公式能解決道德問題嗎？

再說，聲音混在一起，就如同染料混在一個缸裡，你還能分出來？我就不信了！

我感覺有人跟我對話，充滿了質疑和不屑。

那好，我換一個例子，收音機大家都知道吧。

全國幾百家廣播臺，各家都往外發送無線電波。

我們並非生活在多個平行宇宙。因此，這些電波沒有VIP通道，肯定都是混在一起在空中傳播的。就像下面這樣：

那……收音機，可以收聽指定電臺的節目。

這個是機器，它的收音設備，沒有你的耳朵那麼複雜，也沒有神經元，這一點兒靈性也沒有，但它是可以分解指定波段的。

好了，繼續看我表演，說一下聲音的兩個屬性：頻率、振幅。

3.1 聲音的頻率

聲音是由振動產生的，振動一般都是……就……就像這樣：

一個點圍繞著某個相對固定的中心，周期性地移動。

比如，一個彈簧吊著一個小球，上下振動。

如果，一邊記錄時間，一邊記錄位置，其實它的形狀就是弦曲線（我保證這個詞，已是本文最專業的術語），也可以叫波。

有些物體振動得快，1秒鐘反覆來回1000次。有些物體振動的慢，1秒鐘才往返1個周期。

這個單位時間內振動一個周期的次數，我們就叫頻率。

因為材質不同，不同的物體振動的頻率是不一樣，波形也不一樣。

下面是物理課上，敲擊音叉振動的聲波。

下面是用嘴吹試管的聲波。

只要我們聽到的聲音不一樣，基本上它們聲波的頻率也是不一樣的。

就算都是口琴，低音區是這樣的：

高音區是這樣的：

我們發現，高音區比較密集，相同單位內振動的次數更多，也就是頻率大。反之，低音區頻率小，比較稀疏。

你聽到的每種不同類型聲音，都有自己固定的頻率，就像每個地方菜的口味一樣，是有差別的。此處打個標記叫[B]，如果你看不懂，就說從[B]開始，就亂了，來告訴我。

3.2 聲音的振幅

聲音的振幅就是聲音的大小。大小和頻率沒有任何關係。

頻率是某個時間內，推了耳膜多少次。振幅是這次推動，花了多少力氣。

還是拿音叉舉例子，聲音的振幅只影響音量，波形、頻率都不變。你敲出原子彈爆炸的音量，它也是那個形狀。

聲音大時，音叉的波形：

聲音小時，音叉的波形：

這很好理解，不管我小聲說話，還是大聲說話，你都能聽出是我。但是，我大聲說話，你會震得耳朵疼（耳膜遭受一記重拳）。

再來點兒談資吧。我們人類能聽到的頻率範圍是20Hz(1秒鐘振動20個周期)到20000Hz。超過20000Hz為超聲波，低於20Hz為次聲波。我們常說，蝙蝠發出的超聲波，不是因為它聲音太小或太大，導致我們聽不見。其實是因為它振動得太快，蝙蝠已經說了5000字了，但是我們只收到一個「的」。這是沒有意義的。同樣，我們人類能發出的聲音頻率也是有範圍的，範圍在250Hz-4000Hz之間，這是由我們人類聲帶的肉質（額……不知道為啥突然出來這個詞）決定的。

振幅和頻率的區別，此處打個標記叫[C]。

如果你了解了，頻率和振幅這兩個波的屬性，後面就好說了。

四、說傅立葉變換吧：我不抗拒了！

傅立葉發現，這個世界上的人，對事物的理解不透徹，描述的也不科學。

世人都以時間為軸線，來描述事物。比如，描述一段1分鐘的錄音：第1秒說了什麼，第2秒說了什麼……。

世人搖搖頭，嘆了口氣：傅立葉，你想咋著？

4.1 時域

傅立葉說，以時間作為參考的描述，叫時域分析。

比如下面這圖，這是個時域圖。我們看到這1秒內，它很忙，來來回回，從0到1秒跑著，從-1跑到1，反覆了5次。所以，這段波的頻率是5，最大振幅是1。整圖描述的是，每一個時刻的信號值：

如果這段波，不是1秒，而是1個小時，那麼它就是3600個這樣的圖拼在一起。

時域的概念，打個標記叫[D]。不懂的話，就看看表，再看看路上的汽車，剛才在你左邊，1分鐘後到了你的右邊。2分鐘後，它還在原地等紅綠燈，每個時間都有對應的位置。這也是我們普通人認識世界的方式。

4.2 頻域

還是那段波，而如果用頻域來描述，那就是這樣的：

橫坐標表示頻率，縱坐標表示振幅。上面這個圖表示：這裡面有一段波，頻率為5，振幅為1。

傅立葉告訴世人，我這個頻域，可以抵得過時域的千年萬年。兩者說的是同一件事，只是分析的角度和描述手段不一樣。

呵呵哈……哈呵呵，傅立葉冷笑著離開了，他連笑，都帶著波形。

頻域，打個標記叫[E]。

4.3 波的合成和分解

世界上的波，不會是上面說的那麼單純，實際上是很複雜的。

波，根據固定的頻率振動，原本很單純。只是，大家都在同一個空間內振動，相互之間發生了抵消和促進，相互融合，進行疊加，導致它很複雜。

波的疊加，打個標記叫[F]。不明白的話，趕緊評論區輸入[F]，讓我知道，我會加強細節描述。

既然能疊加，那麼能拆解嗎？

其實，是可以的。不只是聽覺，人類的味覺也做到了，你吃一口菜，可以嘗出來裡面有糖，有醋，有辣椒。它的理論基礎就是，味覺具有一定的標準，辣就是辣，混到哪裡都是辣。

波也一樣，大家都是振動，震動就是弦曲線，只是頻率不一樣。

我們可以通過轉啊轉，各種組合，你護攏我，我護攏你，總能拼起來。

規律的波，並非一定得是「U」形，下面這幾種情況，也都是規律的波形。

甚至，下面這個形狀，也是規律的波形。可以拆解為若干組波的疊加。

二維空間裡沒有規律，就去從三維空間裡面找。即便實在無法分解，我們也可以認為它的周期無限長，我有規律，只是本次循環還沒到頭呢？著啥急！

波的分解，不用明白具體是怎麼分的。知道能分就行，打個標記叫[G]。

4.4 時域拆解頻域

一段複雜的波，可以分解成，多段，規律的單純波的集合。

然後，對這些規律的波從頻域進行描述，就有了整段波的譜線圖。

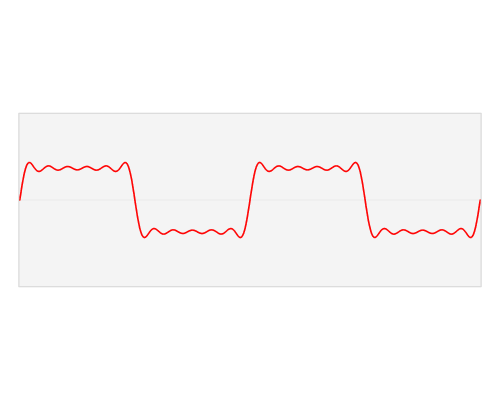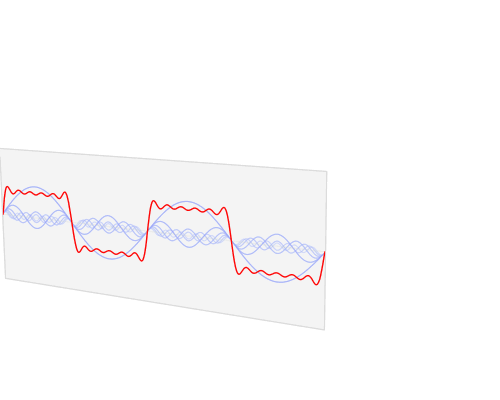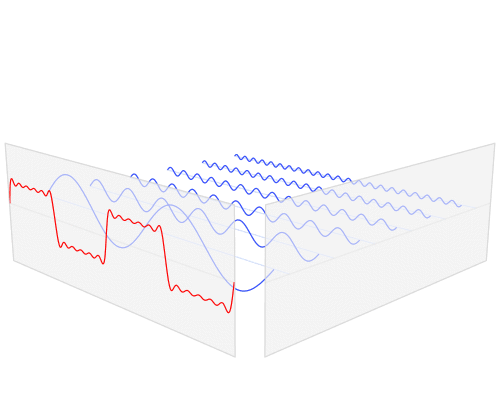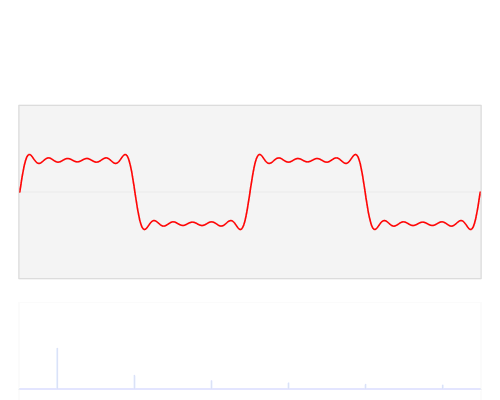
下圖是一個綜述。f指的是頻率維度。這張圖，很清晰地說明了波形、時域和頻域的關係。很多教程，開局就拿出這張圖，可解萬難。但是，我說了這麼久，才敢亮出來。

此圖打個標記叫[H]，還不明白來掐我。

4.5 頻域復原時域

根據頻域，也能復原成時域（此處用理想波，便於理解概念，還有相位等問題，不敢具體展開了）。

上面圖裡綠色的頻率和振幅，可以描述一個波。如果把譜線上描述的波，依次畫出來，然後做疊加。這樣就復原了時域的波形。這個過程就像是泡發木耳。

波的復原，打個標記叫[I]，有疑問請評論（別的平臺複製本文可能不回復，但是掘金TF男孩一定給你回復，且回復的比你問的還要多）。

五、傅立葉變換有什麼用？

傅立葉變換，在生物領域，你已經享受到它的益處了，你能分辨出一段聲音裡不同的聲源，一口食物裡不同的味道。

除此之外，我們可以拿時域轉頻域，對頻域的特徵進行二次加工，然後再恢復成時域，以此來做文章。

比如那些演唱會上調節音效卡的人，如果你高音不足，可以給你升上去，低音太高，可以給你降下來。

舉個例子，比如變聲軟體。把一段音頻，分離出男聲和女聲，將男聲改為女聲的頻率，然後還原回去，實現男聲變女聲。

再比如，聲音壓縮。將一些低頻波形，合成一條。如下圖藍色線條，可以替代其下方的其他多條波形，而又不會影響人們的聽覺判斷，以此實現了數據的壓縮。

除了在音頻和信號的應用之外，在視覺上也有廣泛應用，比如輪廓提取、美顏磨皮等等。

甚至，我還有一個想法，研發一款不會顛簸的汽車：

應用部分，如需討論，打個標記叫[J]。

六、代碼實踐

如果，你已掌握了上面說的傅立葉變換。那麼，下面，我們就要實踐一下了。

實踐的目的在於應用，表示我們已經可以利用代碼，進行傅立葉變換了。這可以加深理解，並儲備知識。

以下代碼，採用python語言演示。

6.1 生成波形

傅立葉變換，是對波形做變換。因此，要變換我們首先得有一段波形。比如這一段音頻，這是單詞「stop」的聲音波形(3個小高峰，s-tɒ-p)：

信息的讀取和繪製都很簡單：

from scipy.io import wavfileimport matplotlib.pyplot as plt# 讀取音頻數據Fs, audio_wave = wavfile.read("stop.wav") # 採樣率 fs, 音頻數據 audio_waveplt.plot(audio_wave) # 繪製音頻數據plt.show

這樣看的不直觀，我們選取開頭的160個點，plt.plot(audio_wave[0:160])來繪製這一小段，這樣看就是線條的波形了：

從總圖看，開頭那部分是一馬平川。但是，當我們放大這部分細節時，我們看到的卻是滿眼的崎嶇和坎坷。

我們看到上面的wavfile.read函數返回兩個值，一個叫採樣率，一個叫音頻數據。

聲音的讀取和波形繪製，此處打個標記叫[K]。

6.1.1 採樣率

採樣率就是採樣的頻率，描述多長時間記錄一次數據。

還記得打點計時器嗎？

那個在紙上打點的頻率，就叫採樣率。

比如，1秒鐘打60個點，採樣率就是60。

60的採樣率，能記錄上信息嗎？

這得看對方信號有多快。

如果對方太慢，會導致一個地方頻繁打點，其實打一個點和打100個點沒有區別，這很浪費。

如果對方太快，可能會記錄不全，甚至它跑了好多周期了，我們一個點都採不上。蝙蝠的超聲波就是頻率太快了，我們的耳膜採樣不上。

下圖是採樣率為1000和100時，記錄的圖：

可見，信號不複雜時，採樣率高和超高，沒有什麼變化，都能記錄全了。區別只是，用1萬個點來描述，還是用100個點來描述。

下圖是採樣率為20時，繪製的同一段信號的圖：

採樣率一旦比信號低(小於信號最高頻的2倍)了，有些信息的細節就記錄不上了。

對於錄音機，我們說，它是否能把聲音的細節記錄上，主要看它的採樣率高不高。

關於採樣率，此處打個標記叫[L]，你是否get全了呢？

為什麼要了解這些概念？因為我們要製造聲波數據，需要先了解它。

為什麼要造數據（這自問自答，我也是不要臉了）？因為我們造的數據，是我們已知的參數，便於我們和求出的結果做對照。

要造數據，還需要了解弦函數sin(θ)。

就是橫軸上一個點，對應縱軸上一個值，把它們畫出來，就是一個波：

6.1.2 繪製波形

現在，我們來搞一系列的橫縱坐標點。

import numpy as np#採樣率，單位時間內採集多少次樣本（1秒內記錄1000次，採樣率1kHz）Fs = 1000 #採樣周期，頻率的倒數，相鄰兩點的時間間隔，1秒打10個點，採樣周期就是0.1秒T = 1/Fs #信號長度，信號有多少個點L = 1200 # 時間軸X軸的集合，這批信號每次採集的時間點t = np.arange(L)*T # 幅度值Y軸的集合，1200個點對應的Y軸的值S = np.sin(2*np.pi*t)

上面代碼，t是橫軸坐標，S是縱軸坐標。我們先來看1秒內發生的故事，因為我們設置的是1秒一個周期，其他時間段都是循環的。

我們的採樣率是1000，也就是1秒記錄1000個點。

1秒內，t的值是[0.000,0.001,0.001,……,1.0],把一個2π（完整周期）分成了1000份。對這1000個點求函數的值，也就是S = [0,…0.5,…1,…0,…-0.5,…-1,…,0]。

如果用代碼畫出來的話。

import matplotlib.pyplot as pltplt.plot(t[:1000], S[:1000])plt.show

數據就是下圖所示：

上面的例子中，1秒進行了一個周期，頻率是1。

如果，我們要一個頻率為5的波形，那又該怎麼整呢？

很簡單，讓S = np.sin(2*np.pi*t*5),裡面乘以5，再畫出來，就是下圖這樣：

如果想要一個頻率為8的波形呢？乘以8就可以了！

關于波形數據的生成和繪製，此處打個標記叫[M]。如果大腦過載的話，要及時上報啊。

下面，我們準備了一組複合波數據，作為測試樣本。

這批樣本，其實就是一段頻率為5的波，疊加一段頻率為20的波。

其中有點插曲（故意設計的），這個頻率為20的波，他的振幅為0.5（頻率5的振幅是1），波形是這樣的。

兩段波相加，混合起來是這樣的：

S_5 = np.sin(2*np.pi*5*t)S_20 = 0.5*np.sin(2*np.pi*20*t)S_25 = S_5 S_20

好了，這個就是我們自己造的測試數據。

下面，我們來做傅立葉變換，看看能不能分析出來它的組成。

關于波的疊加，此處打個標記叫[N]。

6.2 傅立葉變換 FFT

今天，我們是用傅立葉變換，不是寫傅立葉變換。所以過程會很簡單，簡單到就3個字母fft。

python庫scipy.fftpack中有fft，它就是專門處理傅立葉變換的。

from scipy.fftpack import fft# 完成傅立葉變換Y = fft(S_25)# 把結果畫出來p2 = np.abs(Y)p1 = np.abs(Y)[:int(L/2)]# Fs、L是之前生成波形時的採樣率和信號長度f = np.arange(int(L/2))*Fs/L plt.plot(f,2*p1/L) plt.show

採用傅立葉變換，對測試波形進行分析，得出了這個譜線。

從圖上我們看出，整段波裡，存在2個頻率的波形，一個頻率為5，振幅為1；另一個頻率為20，振幅是0.5（剛才就是按照這個規則造的假數據）。

這說明，分析的很對。

此時，我們可以玩耍的就多了。比如增大高頻的頻率，或者把低頻的刪除，然後再還原為波形，就做到了對聲音的增強、提取和調整。

關於譜線，能看懂就行，此處打個標記叫[O]，看不懂來掐我。

等會……這裡面存在一個問題，那就是：這個分析結果，把時間維度給忽略了。

然而，時間是一個很重要的參考。

上面演示的是S20和S5疊加的情況。如果要是S20追加S5呢？意思就是有先後順序，就像這樣：

S_20_5 = np.append(S_20, S_5)

這段波形，先是一段小聲（振幅小）的高頻（頻率大），然後是一段大聲（振幅大）的低頻（頻率小）。

我分析啊，應該先是女生小聲嘀咕，然後男生大聲呵斥。這個時間順序裡面，是包含著故事的。

波形分析裡沒有時間維度，就相當於食品說明裡，只有組成成分，沒有含量佔比。這，沒法判斷它的口味和營養。

於是，短時傅立葉變換就出現了。

6.3 短時傅立葉變換 STFT

本文的畢業考核，就是最終能看懂下面這張圖。

不著急，我慢慢說。

為了加上時間（序列）維度，才有了短時傅立葉。

其實，它的本質還是傅立葉，只是它從時域信號中，依次選取一段樣本，進行傅立葉分析。分析完了，再合併起來，這樣就有了時間維度了。

短時傅立葉變換的調用依然很簡單，比傅立葉變換多一個字母，它是stft。傳入的參數是要分析的波形數據，以及採樣頻率，返回值是：時間t、頻率f、振幅Z。

from scipy.signal import stft# 短時傅立葉變換f, t, Z = stft(S_20_5, fs=1000)# 把結果畫出來z = np.abs(Z)plt.figure(figsize=(10,10))plt.xlabel("author:[email protected] Time(s)")plt.ylabel("frequency")plt.ylim(ymin=0, ymax= 30)plt.title("from https://juejin.cn/user/615370768790158")c = plt.pcolormesh(t, f, z, cmap ='Greens', vmin = 0, vmax = 1)plt.colorbar(c)

由短時傅立葉變換得出數據生成的這個圖，叫三維頻譜圖。

相比於譜線圖，它加入了時間維度。

其中，橫坐標是時間維度，這個時間可以不和波形圖的時間對應。它和上面的fs採樣點參數有關。縱坐標，則表示波形的頻率。它雖然是一幅2維圖，但可以表示3維的數據。

他的第三維度就是色塊的色值，表示振幅。色值越亮，振幅越大。

如何來分析這個圖：

從縱坐標入手：這段信號，包含2段頻率，一段頻率是20，另一段頻率是5。其中20頻率段振幅較小，5頻率段的振幅較大。從橫坐標入手：1.2s之前，只有高頻信號；1.2s之後，高頻消失，出現了低頻信號，低頻音量較大。從振幅入手：聲音較大（色值較重）的主要出現在後半段，且是低頻信號發出，推測是男生發火了。

關於三維頻譜圖的解讀，此處打個標記叫[P]，看不懂就告訴我。

好了，試試畢業考試吧，看下面這幅頻譜圖。這是一段音樂，上面兩個波形是左右聲道，下面火紅的顏色是頻譜，右側坐標是音調（頻率），比如C調，G5調等。

這段音樂，哪段音域最活躍呢？這個歌手是女高音，還是男低音？

七、保命條款

朋友們，我講的很初級，真的，一點都不謙虛。沒講相位，沒講函數的每一個參數，能省就省。這只是為了科普，讓大家知道有這麼一個東西，不但要知道，最好能吸收進去一些知識。學到的知識才是自己的。

本文的目標讀者，就是那些連sin和cos都還給初中數學老師的朋友們。他們真的找不到通俗的資料去學習，但是他們又有強烈的求知慾，儘管很多醫生……不是，很多研究生，大呼他們已經盡力了。

我不會再往深裡講了，因為本身我也不太懂。但是，我相信本文也是能幫到一些人的，尤其本文上傳了將近50張圖，很多動態圖。

如果有錯誤，歡迎大家指正，我會做修改，同時這也是我學習的機會。

如果大家想和我交流，歡迎大家留言，我是掘金社區TF男孩，一位編程表演藝術家，為人民表演編程。如果大家在別的站點看到本文，那可能是轉載，請去掘金找我聊。如有轉載的朋友，請註明出處，讓讀者可以找到作者，請成全兩者。

,