有趣的生日悖論 揭秘23人中兩位一天生日機率超50%
2024-07-12 22:14:49 1
導語:世界上很多事情並不是非黑即白的,有很多東西不能細推,推敲出來就會出現矛盾,也就是大家常說的。有關的問題還有很多,有些人也疑惑,還有等等,下面探秘志小編為大家介紹另外一種神奇的悖論-生日悖論,下面一起了解一下吧。

生日悖論
這個就是指一個房間裡有23個或23個以上的人,那麼至少有兩個人的生日相同的概率要大於50%。也就意味著一個30人的小學班級中,兩人生日一致的可能性更高。假如人數是30的幾倍的話,這個概率更是會大於99%。
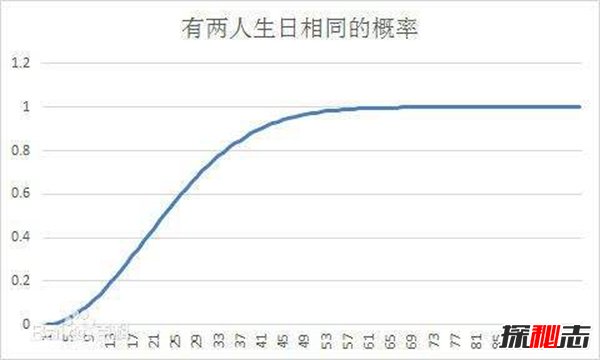
雖然從引起邏輯矛盾方面來看,似乎這個並不算是一種悖論,只有從這個數學事實與一般直覺相牴觸的意義上,它才稱得上是一個悖論。
悖論內容

如果一個房間裡有23個或23個以上的人,那麼至少有兩個人的生日相同的概率要大於50%。這就意味著在一個典型的標準小學班級(30人)中,存在兩人生日相同的可能性更高。對於60或者更多的人,這種概率要大於99%。
不計特殊的年月,如閏二月。
先計算房間裡所有人的生日都不相同的概率,那麼
第一個人的生日是 365選365
第二個人的生日是 365選364
第三個人的生日是 365選363
:
:
:
第n個人的生日是 365選365-(n-1)
所以所有人生日都不相同的概率是:
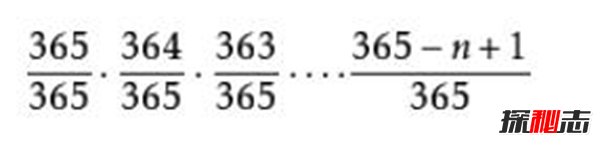
那麼,n個人中有至少兩個人生日相同的概率就是:

所以當n=23的時候,概率為0.507
當n=100的時候,概率為0.999999692751072
對於已經確定的個人,生日不同的概率會發生變化。下面用隨機變量計算:
令X[i,j]表示第i個人和第j個人生日不同的概率,則易知任意X[i,j]=364/365
令事件A表示n個人的生日都不相同
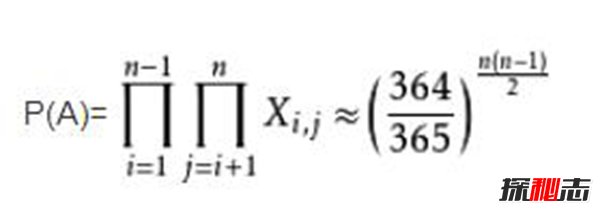
解P(A)=23
相比之下,隨機變量也同樣的簡單易懂而且計算起來要方便得多
理解悖論

這個問題的關鍵在於認識到相同生日的搭配可以是相當多的。比如23個人可以產生23 × 22/2 = 253種不同的搭配,而這每一種搭配都有成功相等的可能。從這樣的角度看,在253種搭配中產生一對成功的配對也並不是那樣的不可思議。
換一個角度,如果你進入了一個有著22個人的房間,房間裡的人中會和你有相同生日的概率便不是50%了,而是變得非常低。原因是這時候只能產生22種不同的搭配。生日問題實際上是在問任何23個人中會有兩人生日相同的概率是多少。
結語:看了這個生日悖論問題,大家是不是覺得和一樣也相當有意思。有些人認為這個悖論不能應用在生活中,實際上並不是這樣,生活中很多東西都運用了這個有關悖論。







